CBSE- Squares and Square Roots-NCERT Solutions
Class VIII Math
NCERT Solution for Squares and Square Roots
NCERT Solution for Squares and Square Roots
EXERCISE 6.1
1. What will be the unit digit of the squares of the following numbers?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 26387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
Sol: (i) ∵ 1 × 1 = I
∴ The unit’s digit of (81)2 will be 1.
(ii) 2 × 2 = 4
The unit’s digits of (272)2 will be 4.
(iii) Since, 9 × 9 = 81
The unit’s digit of (799)2 will be 1.
(iv) Since, 3 × 3 = 9
The unit’s digit of (3853)2 will be 9.
(v) Since, 4 × 4 = 16
The unit’s digit of (1234)2 will be 6.
(vi) Since 7 × 7 = 49
The unit’s digit of (26387)2 will be 9.
(v) Since, 8 × 8 = 64
The unit’s digit of (52698)2 will be 4.
(vi) Since 0 × 0 = 0
The unit’s digit of (99880)2 will be O.
(vii) Since 6 × 6 = 36
The unit’s digit of (12796)2 will be 6.
(x) Since, 5 × 5 = 25
The unit’s digit of (55555)2 will be 5.
2. The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050
Sol: (i) 1057
Since, the ending digit is 7 (which is not one of 0, 1, 4, 5, 6 or 9)
∴1057 is not a perfect square.
(ii) 23453
Since, the ending digit is 7 (which is not one of 0, 1, 4, 5, 6 or 9).
∴23453 is not a perfect square.
(iii) 7928
Since, the ending digit is 8 (which is not one of 0, 1, 4, 5, 6 or 9).
∴7928 is not a perfect square.
(iv) 222222
Since, the ending digit is 2 (which is not one of 0, 1, 4, 5, 6 or 9).
∴222222 is not a perfect square.
(v) 64000
Since, the number of zeros is odd.
∴64000 is not a perfect square.
(vi) 89722
Since, the ending digits is 2 (which is not one of 0, 1, 4, 5, 6 or 9).
∴89722 is not a perfect square.
(viii) 222000
Since, the number of zeros is odd.
∴222000 is not a perfect square.
(viii) 505050
The unit’s digit is odd zero.
∴505050 can not be a perfect square.
3. The squares of which of the following would be odd numbers?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
Sol: Since the square of an odd natural number is odd and that of an even number is an even number.
(i) The square of 431 is an odd number.
[∵ 431 is an odd number.]
(ii) The square of 2826 is an even number.
[∵ 2826 is an even number.]
(iii) The square of 7779 is an odd number.
[∵ 7779 is an odd number.]
(v) The square of 82004 is an even number.
[∵ 82004 is an even number.]
4. Observe the following pattern and find the missing digits.
112 =
121
1012 =
10201
10012 =
1002001
1000012 =
1.............2 ............. 1
100000012 =
............
Sol: Observing the above pattern, we have
(i) (100001)2 - 10000200001
(ii) (10000001)2 = 100000020000001
5. Observe the ,following pattern and supply the missing number.
112 = 121
1012 = 10201
101012 = 102030201
10101012 =
..............2 = 10203040504030201
Sol: Observing the above, we have
(i) (1010101)2 = 1020304030201
(ii) 10203040504030201 = (101010101)2
6. Using the given pattern, find the missing numbers.
12 + 22 + 22 = 32
22 + 32 + 62 = 72
32 + 42 + 122 =132
42 + 52 + —2 = 212
52 + —2 + 302 = 312
62 + 72 + —2 = —2
Note: To find pattern:
Third number is related to first and second number. How?
Fourth number is related to third number. How?
Sol: The missing numbers are
(i) 42 + 52 + 202 = 212
(ii) 52 + 22 + 302 = 312
(iii) 62 + 72 + 422 = 432
7. Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 +19
Sol: (i) The sum of first 5 odd = 52
= 25
(ii) The sum of first 10 odd numbers = 102
= 100
(iii) The sum of first 12 odd numbers = 122
= 144
8. (i) Lxpress 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.
Sol: (i) 49 = 72 = Sum of first 7 odd numbers
= 1 + 3 + 5 + 7 + 9 + 11 + 13
(ii) 121 = 112 = Sum of first 11 odd numbers
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
9. How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100
Sol: Since between n2 and (n + 1)2, there are 2n non-square numbers.
∴ (i) Between 122 and 132, there are 2 × 12, i.e. 24 numbers
(ii) Between 252 and 262, there are 2 × 25, i.e. 50 numbers
(iii) Between 992 and 1002, there are 2 × 99, i.e. 198 numbers
EXERCISE 6.2
1. Find the square of the following numbers.
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46
Sol: (i) (32)2 = (30 + 2)2
= 302 + 2(30)(2) + (2)2
= 900 + 120 + 4 = 1024
(ii) (35)2 = (30 + 5)2
= (30)2 + 2(30)(5) + (5)2
= 900 + 300 + 25
= 1200 + 25 = 1225
Second method
352 = 3 × (3 + 1) × 100 + 25
= 3 × 4 × 100 + 25
= 1200 + 25 = 1225
(iii) (86)2 = (80 + 6)2
= (80)2 + 2(80)(6) + (6)2
= 6400 + 960 + 36 = 7396
(iv) (93)2 = (90 + 3)2
= (90)2 + 2(90)(3) + (3)2
= 8100 + 540 + 9 - 8649
(v) (71)2 = (70 + 1)2
= (70)2 + 2(70)(1) + (1)2
= 4900 + 140 + 1 = 5041
(vi) (46)2 = (40 + 6)2
= (40)2 + 2(40)(6) + (6)2
= 1600 + 480 + 36 = 2116
2. Write a Pythagorean triplet whose one member is
(i) 6
(ii) 14
(iii) 16
(iv) 18
Sol: (i) Let 2n =6 ∴n=3
Now, n2 – 1 = 32 –1 = 8
and n2 + 1 = 32 + 1 = 10
Thus, the required Pythagorean triplet is 6, 8, 10.
(ii) Let 2n = 14 ∴n = 7
Now, n2 – 1 = 72 – 1 = 48
and n2 + 1 = 72 + 1 = 50
Thus, the required Pythagorean triplet is 14, 48, 50.
(iii) Let 2n = 16 /n = 8
Now, n2 – 1 = 82 – 1
= 64 – 1 = 63
and n2 + 1 = 82 + 1
=64 + 1 = 65
∴ The required Pythagorean triplet is 16, 63, 65.
(iv) Let 2n = 18 n = 9
Now, n2 – 1 = 92 – 1
=81 – 1 = 80
and n2 + 1 = 92 + 1
= 81 + 1 = 82
∴ The required Pythagorean triple is 18, 80, 82.
EXERCISE 6.3
1. What could be the possible ‘one’s digits of the square root of each of the following numbers?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Sol: The possible digit at one’s place of the square root of:
(i) 9801 can be 1 or 9.
[∵ 1 × 1 = 1 and 9 × 9 = 81]
(ii) 99856 can be 4 or 6.
[∵ 4 × 4 = 16 and 6 × 6 = 36]
(iii) 998001 can be 1 or 9.
(iv) 657666025 can be 5. [∵ 5 × 5 = 25]
2. Without doing any calculation, find the numbers which are surely not /)er/’c’t squares.
(i) 152
(ii) 257
(iii) 408
(iv) 441
Sol: We know that the ending digit of perfect square is 0, 1, 4, 5, 6, and 9.
∴ A number ending in 2, 3, 7 or 8 can never be a perfect square.
(i) 153, cannot be a perfect square.
(ii) 257, cannot be a perfect square.
(iii) 408, cannot be a perfect square.
(iv) 441, can he a perfect square.
Thus, (1) 153, (ii) 257 and (iii) 408 are surely not perfect squares.
3. Find the square roots of. 100 and 169 by the method of repeated subtraction.
4. Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729
(ii) 400
(iii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
5. For each of the Following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
Sol: (i) We have
252 = 2 × 2 × 3 × 3 × 7
∵ The prime factor 7 has no pair.
∴ [252] × 7= [2 × 2 × 3 × 3 × 7] × 7
or 1764 = 2 × 2 × 3 × 3 × 7 × 7
Thus, the required smallest whole number = 7
Also, the square root of 1764 is 42.
(ii) We have
Thus, the required smallest whole number = 5
Also, the square root of 900 is 30.
(iii) We have
Thus, the required smallest whole number = 7
Also the square root of 7056 is 84.
(iv) We have
(v) We have
(vi) We have
6. For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained.
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
Sol: (i) 252
We have
∵ The prime factor 7 is unpaired, so the given number should be divided by 7.
(ii) 2925
We have
∵ The prime factor 13 is unpaired, so the given number should be divided by 13.
(iii) 396
We have
(iv) 2645
We have
∵ The prime factor 5 is unpaired.
∴ Dividing the given number by 5, we have
or 529 = 23 × 23
Thus, 529 is a perfect square, and 529 = 23.
(iv) 2800
We have
(v) 1620
We have
1620 = 2 × 2 × 3 × 3 × 3 × 3 ×5
∵ The prime factor 5 is unpaired.
∴ Dividing the given number by 5, we have
7. The students of Class VIII of a school donated Rs 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Sol: Let the number of students = x
Each student donated Rs x.
Total amount donated by the class = Rs x × x = Rs x2
Thus, x2 = 2401
8. 2025 plants are to be planted in a garden in such a tivav that each row contains as many plants as the number of rows. Find the number of row and the number of plants in each row
Soln: Let the number of rows = x
∴ Number of plants is a row = x
So, the number of plants to be planted = x × x = x2
Thus, the required number of rows = 45
Also, number of plants in a row = 45.
9. Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
Sol: We know that LCM is the smallest number divisible by all its factors.
Since, LCM of 4, 9 and 10 = 2 × 2 × 9 × 5 = 180
But 180 is not a perfect square.
Again,
∴ 180 = 2 × 2 × 3 × 3 × 5
∵ All the prime factors of 900 are paired.
∴ 900 is a perfect square.
Thus, the required number = 900.
10. Find the smallest square number that is divisible by each of the numbers 8, 15 and 20
Sol: The smallest number divisible by 8, 15 and 20 is their LCM.
We have LCM = 2 × 2 × 5 × 2 × 3 = 120
But 120 is not a square number.
Now, to make it a perfect square, we have
120 = 2 × 2 × 2 × 3 × 5
or [120] × 2 × 3 × 5 = [2 × 2 × 2 × 3 × 5] × 2 × 3 × 5
or 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
All factors of 3600 are paired. Therefore, 3600 is a perfect squared.
∴ The required number = 3600.
EXERCISE 6.4
1. Find the square root of each of the following numbers by Division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
2. Find the number of digits in the square root of each of the. following numbers (without any calculation).
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
Sol: If ‘n’ stands for number of digits in the given number, then
3. Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Here, number of decimal places, are already even.
∴ We mark off the periods and find the square root.
Here, number of decimal places are already even.
Therefore, we mark off the periods and find the square root.
4. Find the least nti,nllc’r” which must be subtracted from each of the following numbers. so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
Sol: (i) On proceeding to find the square root of 402, we have
Since, we get a remainder 2
The required least number to be subtracted from 402 is 2.
(ii) Since, we get a remainder of 53
The least number to be subtracted from the given number - 53 84
(iii) Since, we get a remainder 1.
The smallest number to be subtracted from the given number = 1
(iv) Since, we get a remainder 41.
The required smallest number tcI be subtracted from the given number = 41
(v) Since, we get a remainder 31,
The required smallest number to he subtracted from om the given number = 31
5. Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect ware so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
Sol: (i) Since, we get a remainder 41.
and next square number is 23.
∴ The required number to be added = 232 – 525
= 529 – 525 = 4
Now, 524 + 4 = 529, and = 23.
(ii) Since, we get a remainder 69.
and next square number is 422.
∴ The required number to be added = 422 – 1750
= 1764 – 1750 = 14
Now, 1750 + 14 = 1764, and 
(ii) Since, we get a remainder 27.
(iv) Since, we get a remainder, 61.
Next square number = 43
The required number to be added = (43)2 – 1825
= 1849 – 1825 = 24
Now, 1825 + 24 = 1849, and 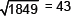
(v) Since, we get a remainder 12.
6. Find the length of the side of a square whose area is 441 m2.
Sol: Let the side of the square = x metre
Area = side × side
7. In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC.
(b) If AC = 13 cm, BC = 5 cm, find AB. Solution:
Sol:
REMEMBER
I. In a right triangle, the longest side is called the hypotenuse.
II. (Hypotenuse)2 = [Sum of the squares of other two sides]
(a) ∠B = 90°
Hypotenuse = AC
AC2 = AB2 + BC2
= 82 + 62
= 64 + 36 = 100
AC = 10
Thus, AC = 10 cm
(b) Here B = 90°
∴ Hypotenuse = AC
AC2 = AB2 + BC2
or 132 = AB2 = 52
= 169 – 25 = 144
or AB = 12
Thus, AB = 12 cm
8. A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more or this.
Sol: Since, the number of plants in a row and the number of columns are the same.
∴ Their product must be a square number.
The gardener has 1000 plants.
1000 is not a perfect square, and (31)2 < 1000
(There is a remainder of 39).
Obviously the next square number = 32
Number of plants required to be added = (32)2 – 1000
= 1024 – 1000 = 24
9. There are 500 children in a school. For a P T drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children this arrangement.
Sol: Since, the number of rows and the number of columns are same.
Total number (i.e. their product) must be a square number, we have
Since, we get a remainder of 16
500 > (22)2 or 500 – 16 = (22)2
Thus, the required number of children to be left out = 16
